大振幅AM変調信号受信動作,
DSB変調波受信動作,
無変調キャリア受信動作,
検波音質最適化の方式
1. 変調率100%以上の大振幅のAM変調波の検波特性
記事[1]で示したように、AM送信局/放送局の変調度が100%以上(変調指数が1.0以上)でも、変調波信号は歪み信号成分を含んでいない。
言い換えれば、通称「過変調」と呼ばれているAM変調波には、電気的関数として歪み信号成分は存在していない。
そうした過変調と呼ばれるAM変調波は、ダイオード検波回路による従来の「包絡線検波理論」によれば、AM変調波の包絡線が、電圧のマイナス側がカットされて、検波信号は歪むと現在でも言われている。[2]
では、実際にそうした「過変調」と呼ばれているAM変調波を、ダイオード検波回路はどのように検波動作するかをここで解析する。
図1.1 ,図1.2,図1.3 は、いずれも 変調率100%以上の大振幅のAM変調波を受信した場合の、ダイオード検波回路の出力電圧と、その周波数成分のスペクトルをFFT解析で見たものである。
 |
| 図1.1 変調率200%以上の大振幅のAM変調波の検波特性 |
図1.1にて、従来の「包絡線検波理論」によれば、AM変調波の包絡線が、電圧のマイナス側がカットされて、検波信号は歪み、マイナス側の象限にある包絡線が、検波電圧に現れることになっているが、1KHz 変調率200%以上の検波信号には、そうした「マイナス側の包絡線が現れる現象」が出ていない。
すなわち、「過変調」現象は、ここのダイオード検波回路の動作条件では発生していない。
右側の周波数スペクトル解析に現れている1KHzの高調波成分 2KHz,3KHz・・・の整数倍の信号成分は、ダイオード電流の指数関数特性に由来して計算であらかじめ予測済の高調波歪みであるが[3]、この歪み成分は、前述の「マイナス側の包絡線」が存在しないために、その歪みは無いことになる。
図1.1では、「過変調」と呼ばれてきている受信入力電圧の信号形状がわかりやすいように、赤で変調度200%の信号を前面に表示させた。
 |
| 図1.2 変調率100%以上の大振幅のAM変調波の検波特性 その2 |
図1.2では、最大の変調率と考えられてきている変調度100%の受信入力信号を水色で前面に表示し、「過変調」と呼ばれてきている受信入力電圧を背面に表示した。
いずれも、変調度が100%以上の信号を受信しているが、検波出力波形には、前述の「マイナス側の包絡線は現れていない。
すなわち、図1.1と同様に、「過変調」現象は、これら図1.2,図1.3のダイオード検波回路条件でも発生していない。
 |
| 図1.3 変調率100%以上の大振幅のAM変調波の周波数スペクトル |
図1.3には、受信されたAM変調波のスペクトル成分を、キャリアを中心にしてUSB側、LSB側にギャリア信号よりも大きな電圧が含まれていることをFFT解析にて表示したものである。
図1.3では、従来用語の意味において、明らかに「過変調」の送信波が受信されているが、ダイオード検波の検波出力電圧には、前述の「マイナス側の包絡線は現れていない。
(すなわち、過変調の現象は発生していない。)
そうであれば、どのような条件ならば、「過変調」に見える(見間違う)現象が、検波回路出力に現れるだろうか? それについて、項番#4に説明する。
2. DSB変調波の検波動作
ダイオード検波回路をもったラジオや受信機で、DSB変調、またはSSB変調の電波を受信すると、「モガモガ」という音声が聞こえる現象は良く知られている。
その「モガモガ」の音が、どのような仕組みで発生しているかを、図2.1,図2.2を使って説明する。
図1.1では、受信電波の電圧源として、キャリア信号=0[V]として、USB信号、USB信号として、1KHzのサイン波をベースバンド信号とするDSB変調波電圧源(疑似DSB変調送信機)を3個のサイン波の加算された電圧源で構成し、そのDSB変調信号を、ダイオード検波回路に入力している。
このようにDSB変調波では、キャリア信号成分が無い。
検波出力には、USB信号とUSB信号の周波数差分である2KHzと、その高調波が現れている。
この現象は、ダイオードの高周波特性である周波数変換動作と、ダイオード電流の指数関数特性により発生している。
このダイオードの周波数変換動作は、ダイオードミキサについての特性として既に良く知られている。
AM変調波の受信では、キャリア信号とUSB信号間、キャリア信号とLSB信号間のそれぞれの周波数変換で1KHzの検波信号が現れるが、DSB変調信号受信では、キャリア信号が存在しないために、このように変調波成分USB,LSB成分同士が、周波数変換動作を起こす。
キャリア信号が無いため、DSB変調波は、ダイオード検波回路ではベースバンド信号が復調されず、変調波成分USB,LSB成分同士が、周波数変換動作で、低周波領域に出力される。
図2.2は、図2.1の検波出力信号の時間軸を拡大し、また、ここでは存在しないキャリア周波数を中心にした、受信されたDSB変調波のLSB信号とUSB信号の周波数スペクトラム分布を、FFT解析にて周波数軸の周波数幅を狭帯域で見たものである。
赤線、青線、緑線の順で、それぞれUSB,LSB信号成分とその検波出力の電圧を上昇させている。
左下の回路図の下のグラフは、上側が、入力されるDSB変調信号、下側が検波電圧である。
検波電圧は、入力されるDSB信号電圧の上昇により、赤、青、緑の順番で上昇し、それぞれの検波信号のグラフ線は細かく振動しているのが見られる。
この検波信号の細かい振動は、次の図2.3に時間軸を拡大して表示し、その細かい振動を示した。
図2.3は、赤線の検波信号の時間軸を拡大して表示した。
このように細かく振動している周波数の実体は、FFT解析結果を見ると、LSB成分、USB成分の周波数と完全に一致している。
すなわち、検波出力電圧は、ベースバンド1kHzに対し、2KHzの低周波の太い線に見えていたものが、時間軸を拡大すると、LSB/USB周波数成分の細かい高周波変調波の正弦波で構成されていることがわかる。
実際の音声や音楽のベースバンド信号は、多数の正弦波の多重周波数バンドを形成している。このため、多重周波数成分のDSB変調波の変調波信号同士が複雑に絡み合った周波数変換動作がダイオード内部で起こるので、モガモガと聞こえる。
3. 無変調AM波(キャリア)の検波動作
ダイオード検波回路をもったラジオや受信機で、アナウンサが何もしゃべっていない、音楽も流していない無変調状態のキャリア波を受信すると、雑音が少なくなり、無音になる現象を、図3.1,図3.2 を使って説明する。
一見して、キャリア信号は、単なるDC電圧に変換されているので、この検波動作は、商用交流電源の整流回路の動作と同じと見間違えてしまう。
ところが、この検波回路で起こっているのは、そうした交流の整流とは全く性質の異なる電気現象が起こっている。
別記事で書いたように、検波回路負荷のRC並列回路からコンデンサを除くと、負荷抵抗両端には、同じ電圧で、プラスとマイナス両方の高周波電圧が現れる。
図1.3では、従来用語の意味において、明らかに「過変調」の送信波が受信されているが、ダイオード検波の検波出力電圧には、前述の「マイナス側の包絡線は現れていない。
(すなわち、過変調の現象は発生していない。)
そうであれば、どのような条件ならば、「過変調」に見える(見間違う)現象が、検波回路出力に現れるだろうか? それについて、項番#4に説明する。
2. DSB変調波の検波動作
ダイオード検波回路をもったラジオや受信機で、DSB変調、またはSSB変調の電波を受信すると、「モガモガ」という音声が聞こえる現象は良く知られている。
その「モガモガ」の音が、どのような仕組みで発生しているかを、図2.1,図2.2を使って説明する。
 |
| 図2.1 DSB変調波の検波動作 |
図1.1では、受信電波の電圧源として、キャリア信号=0[V]として、USB信号、USB信号として、1KHzのサイン波をベースバンド信号とするDSB変調波電圧源(疑似DSB変調送信機)を3個のサイン波の加算された電圧源で構成し、そのDSB変調信号を、ダイオード検波回路に入力している。
このようにDSB変調波では、キャリア信号成分が無い。
検波出力には、USB信号とUSB信号の周波数差分である2KHzと、その高調波が現れている。
この現象は、ダイオードの高周波特性である周波数変換動作と、ダイオード電流の指数関数特性により発生している。
このダイオードの周波数変換動作は、ダイオードミキサについての特性として既に良く知られている。
AM変調波の受信では、キャリア信号とUSB信号間、キャリア信号とLSB信号間のそれぞれの周波数変換で1KHzの検波信号が現れるが、DSB変調信号受信では、キャリア信号が存在しないために、このように変調波成分USB,LSB成分同士が、周波数変換動作を起こす。
キャリア信号が無いため、DSB変調波は、ダイオード検波回路ではベースバンド信号が復調されず、変調波成分USB,LSB成分同士が、周波数変換動作で、低周波領域に出力される。
 |
| 図2.2 DSB変調波の検波動作と、検波信号のスペクトル成分 その1 |
図2.2は、図2.1の検波出力信号の時間軸を拡大し、また、ここでは存在しないキャリア周波数を中心にした、受信されたDSB変調波のLSB信号とUSB信号の周波数スペクトラム分布を、FFT解析にて周波数軸の周波数幅を狭帯域で見たものである。
赤線、青線、緑線の順で、それぞれUSB,LSB信号成分とその検波出力の電圧を上昇させている。
左下の回路図の下のグラフは、上側が、入力されるDSB変調信号、下側が検波電圧である。
検波電圧は、入力されるDSB信号電圧の上昇により、赤、青、緑の順番で上昇し、それぞれの検波信号のグラフ線は細かく振動しているのが見られる。
この検波信号の細かい振動は、次の図2.3に時間軸を拡大して表示し、その細かい振動を示した。
 |
| 図2.3 DSB変調波の検波動作と、検波信号のRC回路での振動電圧波形 |
図2.3は、赤線の検波信号の時間軸を拡大して表示した。
このように細かく振動している周波数の実体は、FFT解析結果を見ると、LSB成分、USB成分の周波数と完全に一致している。
すなわち、検波出力電圧は、ベースバンド1kHzに対し、2KHzの低周波の太い線に見えていたものが、時間軸を拡大すると、LSB/USB周波数成分の細かい高周波変調波の正弦波で構成されていることがわかる。
実際の音声や音楽のベースバンド信号は、多数の正弦波の多重周波数バンドを形成している。このため、多重周波数成分のDSB変調波の変調波信号同士が複雑に絡み合った周波数変換動作がダイオード内部で起こるので、モガモガと聞こえる。
3. 無変調AM波(キャリア)の検波動作
ダイオード検波回路をもったラジオや受信機で、アナウンサが何もしゃべっていない、音楽も流していない無変調状態のキャリア波を受信すると、雑音が少なくなり、無音になる現象を、図3.1,図3.2 を使って説明する。
 |
| 図3.1 無変調AM波(キャリア)の検波動作 その1 |
一見して、キャリア信号は、単なるDC電圧に変換されているので、この検波動作は、商用交流電源の整流回路の動作と同じと見間違えてしまう。
ところが、この検波回路で起こっているのは、そうした交流の整流とは全く性質の異なる電気現象が起こっている。
別記事で書いたように、検波回路負荷のRC並列回路からコンデンサを除くと、負荷抵抗両端には、同じ電圧で、プラスとマイナス両方の高周波電圧が現れる。
これは、ダイオードの高周波特性の特徴で、ダイオードでは高周波周波数領域では、高周波電圧に対する利得が上昇し、殆ど貫通するような性質が見られる。
(この特性は交流の整流では周波数が低いために出てこない。)
この性質を利用したのが高周波ダイオードスイッチとして知られている。[3]
検波回路の負荷を抵抗にコンデンサを加え、RC並列回路にすると回路動作は激変し、キャリア信号等の高周波がコンデンサを通過してグランドに落ち、入力される高周波電圧より大きくドロップしたDC電圧がRC並列回路に現れる。[4]
 |
| 図3.2 無変調AM波(キャリア)の検波動作 その2 |
このDC電圧が現れる現象は、一見すると交流の整流に見えるが、上の緑、青、赤線のDC電圧は細かいキャリア周波数によるなめらかな波打つサイン波の信号で形成されている。
そのキャリア周波数の存在は、FFT解析上のキャリア周波数点で、鋭いピークに現れている。
このように検波動作は整流動作とは全く異なる電気現象である。
RC並列回路はローパスフィルタとしての性質を持ち、そのRC並列回路の過度現象として、AM変調波、DSB変調波の高周波信号成分で、細かい高周波電圧振動を起こしている。[5]
4. 過変調と見間違う検波動作現象の再現とダイオード検波の高音質最適化方式
過変調と見間違う現象を再現したものを図4.1に示し、変調率が100%以下で、最も検波歪みが少なくする音質を最適化する方法を図4.2に示す。
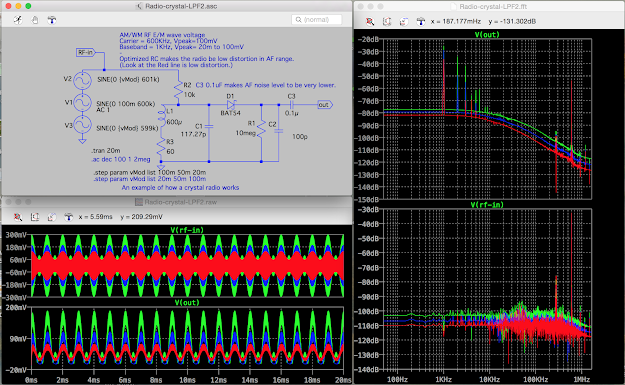 |
| 図4.1 過変調と見間違う検波動作現象の再現 |
図4.1で、変調度40%の赤線は、なめらかな1KHzのベースバンド信号のサイン波として検波され、その周波数スペクトラムは、高調波歪み成分が大変少ない。
赤線に対して、変調度を大きくして100%を超えると、包絡線のマイナス側に現れていたものが、プラス側の象限に顔を出す現象が見られる。
この現象が、歪みの無いはずの送信波が、あたかも送信波が歪んでいるような錯覚(「過変調=音が歪む」)を与える。
 |
| 図4.2 ダイオード検波の高音質最適化方式 |
このような過変調に錯覚する現象が現れる条件は、図4.2のように、RC並列回路の遮断周波数を5KHz程度の高めの音声周波数上端に移動させるものであることがわかった。
図4.2では、検波回路の利得は0Hzから3KHz程度までフラットで、AM変調での上限と考えられる4.5KHzでも利得差は非常に小さく回路構成できる。
このため、結果的にこうした音声の高域を通過させるようなローパスフィルタ特性を持たせると、ダイオード検波回路の音質は高域まで綺麗に出て良い音質に感じて聞こえるようになると考えられる。
5. RC型LPF(ローパスフィルタ)を負荷にしたダイオード検波回路の動作
ダイオード検波回路の負荷には、ローパスフィルタ特性を持つRC並列回路が使用される。
この負荷を、RC直列回路のローパスフィルタで交替できるか否かを判断する計算を行った。
 |
| 図5. RC型LPF(ローパスフィルタ)を負荷にしたダイオード検波回路の動作 |
ダイオード検波回路の負荷に、RC直列回路のローパスフィルタを使用すると、受信感度が大きく下がってしまうことが分かった。
原因は、Rが大きいので直列RC回路では、R両端の電圧降下が大きいため、その分、出力になるC両端電圧が下がってしまうことによる。
このようにRC直列回路のローパスフィルタで交替すると受信特性が劣化してしまう。
引用記事
現在、ここを編集中(暫定公開のため)






