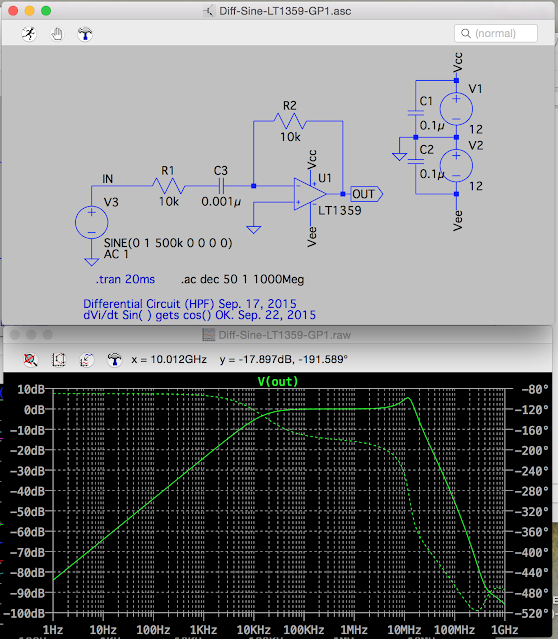
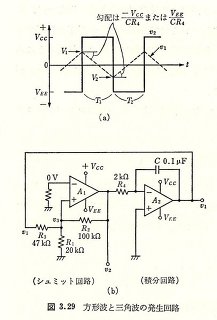
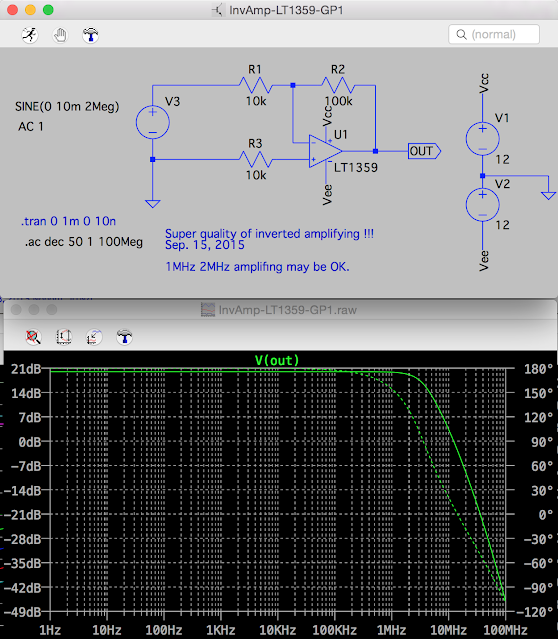
非常に不思議な計算に思えますが、これを好機と前向きにとらえ、ラプラス変換と逆変換を使った検波回路の解析をしてみるのが良いかなと思います。
ラプラス変換を学習または復習できる良いサイトを見つけました。
http://www.jeea.or.jp/course/01.html
ダイオードの物性は、直流特性は良く知られている一方で、私も含め、特に交流特性についてほとんど理解がすすんでいないように思えます。
ダイオードの持っている乗算器に似た物性(ネピア数の指数関数による電圧ー電流特性に基づく)は、数学的計算が失敗している事例も見ました。
ラジオが発明されてもう長い年月がたっていますが、使えてしまっている、実用になるので特に困らないということからか、置き去りにされてきた課題のように考えています。
---対象理論の検証と再現性の確認結果---
図1.1−図1.3に対象理論による伝達関数を用い、AM変調波のダイオード検波が起こるか否かを検証した。その結果、記述された伝達関数によるダイオード検波動作は再現できなかった。
図1.1 伝達関数によるAM変調波のダイオード検波が起こるか否かの検証結果
図1.2 図1.1にFFT解析結果を追加
図1.2 図1.2にFFT解析結果のAM変調波中心周波数近傍を拡大表示
図1.3 図1.1 1.2 のAC解析結果
図1.3 から、600[KHz]への同調動作はしている結果が得られたが、最重要のかなめとなる検波動作による復調電圧は、現在のところは、再現できない結果となった。
上記伝達関数にダイオードの電流式と、ダイオード後のRC並列回路の式が漏れているように考えられる。
ダイオード電流式は、テイラー展開式の近似式で加えれば、伝達関数に盛り込めるかもしれない。
(これは今後の課題とします。)時間の無駄?。
図2.に対象理論の導いた回路図のラジオ動作の過渡解析結果を示した。
AM検波動作は再現できなかった。
図2. 記載されたダイオード検波回路図による回路動作の検証結果
他方のアプローチとして、本ブログで示しているダイオード検波式回路の過渡解析結果、AC解析を、図3〜図4.2に示した。
いずれも期待するAM変調の検波動作が再現した。
図3. 標準的ダイオード検波ラジオ回路の動作確認(期待動作する。)
図4.1 同調回路無しのダイオード検波ラジオ回路の過渡解析・動作確認(期待動作する。)
図4.2 同調回路無しのダイオード検波ラジオ回路のAC解析・動作確認(期待動作する。)
上記結果を比較すると、LTspiceの計算方式が大変優れているように見える。
参考文献:
[1] ラプラス変換を使ったゲルマニウムラジオの解析記事
http://www.yobology.info/text/cristal_radio/cristal_radio.htm
http://www.mnc.toho-u.ac.jp/v-lab/yobology/cristal_radio/cristal_radio.htm
http://www.mnc.toho-u.ac.jp/v-lab/yobology/cristal_radio/cristal_radio.htm
Rev. 0.1 12/18, 2016
検討対象の検波理論の論理検証結果と、回路動作の再現性の確認結果を追記
Rev. 0.2 12/23, 2016
検討対象の検波理論の論理検証結果を再検証。図1.1-1.3改訂と追加。
現在のところ対象理論の再現性に困難が伴う。
Rev.0.3 9/3, 2017
ダイオードは非線型素子で、直流ではi(t)=Is*(exp(V(t)/VT)-1)の電流特性になるが、交流では周波数が上がるほど、高周波を貫通する特性が出てきてしまうので、この式はそのままでは使えない。
ダイオードの非線形特性からは、基本的にはダイオード検波回路を、LTI(Linear Time Invaliant)システムとしての扱いができない。
LTIシステムに近似するには、入力電圧範囲を狭くして、i(t)=K*V(t)のように線形特性に近似すれば、この計算値は直線比例の抵抗となり、周波数変換が発生しないため、ベースバンド信号成分は出す周波数変換動作ができなくなる。
2波の周波数の異なるサイン関数の乗算ではじめて周波数変換が起こるので、ダイオード電流式の指数関数式のテーラー展開近似はどうしても2次電圧乗算式が必須になる。
これは線形でない二次関数以上の関数なので、ダイオード検波回路はけしてLTIシステムに近似できない恐れがある。
H(s)=Laplace{y(t)}/Laplace{u(t)}
入力AM変調電圧:U(t)=Vc(Vdc+Vs*cos(ωs*t)}*sin(ωc*t)
出力検波電圧の近似値:y(t)=K*sin(ωs*t)
と仮定して、伝達関数H(s)が求まる?
ただし、ベースバンド変調波=Vs*cos(ωs)は、一般化すると次のフーリエ級数
x(t)=ΣAi*cos(ωi*t)+Bi*sin(ωi*t) (i=0 to N))
入力関数u(t)が時刻で複雑に非線形に動的に変化するので、一意なるH(s)は求まらないかもしれない。
基礎的には、上記アプローチ法は、ダイオードの存在を無視しているので誤り。
素直にspiceで計算するのが、最も現実に近い精度の高い計算結果になるのが、はっきりしてきたので、そもそも、LTIシステムでないものを伝達関数で計算しようとする考えが、もともとが間違ったものか? 時間の無駄かもしれない。
Return to INDEX
Rev. 0.2 12/23, 2016
検討対象の検波理論の論理検証結果を再検証。図1.1-1.3改訂と追加。
現在のところ対象理論の再現性に困難が伴う。
Rev.0.3 9/3, 2017
ダイオードは非線型素子で、直流ではi(t)=Is*(exp(V(t)/VT)-1)の電流特性になるが、交流では周波数が上がるほど、高周波を貫通する特性が出てきてしまうので、この式はそのままでは使えない。
ダイオードの非線形特性からは、基本的にはダイオード検波回路を、LTI(Linear Time Invaliant)システムとしての扱いができない。
LTIシステムに近似するには、入力電圧範囲を狭くして、i(t)=K*V(t)のように線形特性に近似すれば、この計算値は直線比例の抵抗となり、周波数変換が発生しないため、ベースバンド信号成分は出す周波数変換動作ができなくなる。
2波の周波数の異なるサイン関数の乗算ではじめて周波数変換が起こるので、ダイオード電流式の指数関数式のテーラー展開近似はどうしても2次電圧乗算式が必須になる。
これは線形でない二次関数以上の関数なので、ダイオード検波回路はけしてLTIシステムに近似できない恐れがある。
H(s)=Laplace{y(t)}/Laplace{u(t)}
入力AM変調電圧:U(t)=Vc(Vdc+Vs*cos(ωs*t)}*sin(ωc*t)
出力検波電圧の近似値:y(t)=K*sin(ωs*t)
と仮定して、伝達関数H(s)が求まる?
ただし、ベースバンド変調波=Vs*cos(ωs)は、一般化すると次のフーリエ級数
x(t)=ΣAi*cos(ωi*t)+Bi*sin(ωi*t) (i=0 to N))
入力関数u(t)が時刻で複雑に非線形に動的に変化するので、一意なるH(s)は求まらないかもしれない。
基礎的には、上記アプローチ法は、ダイオードの存在を無視しているので誤り。
素直にspiceで計算するのが、最も現実に近い精度の高い計算結果になるのが、はっきりしてきたので、そもそも、LTIシステムでないものを伝達関数で計算しようとする考えが、もともとが間違ったものか? 時間の無駄かもしれない。
Return to INDEX