しかし、実際はそうではなかった。
実際のSDRは、ハードウェアもソフトウェアも極めてシンプルで、わかりやすい構成と、方式がとられていた。
引用:
http://www.ni.com/tutorial/14705/ja/
ソフトウェア無線向けNI USRP-293xで、グローバル同期/クロック同期を実現
(出典:(Copyright by National Instruments inc. さん))
上図は、(C)National Instruments社さんの、GNU Radio USRP と呼ばれるソフトウェア無線機用のハードウェア構成図。
アンテナ端子 RX2 から入力された受信電波は、RF Switch 通過後、LNA(Low Noise Amplifier),Drive Amp で電圧増幅された後、乗算記号で書かれた2個のアナログ乗算器に
0度位相、90度位相差のある2相のOSC(局部発振器/直交発振器)からの正弦波電圧と、アナログ乗算が行われた信号が、それぞれ直交する実信号電圧成分(I信号、Q信号)が取り出されて、LPF(Low Pass Filter)で余分な信号を除去した後、ADC(ADコンバータ)でアナログ電圧がデジタルデータに変換され、Ethernet経由でパソコンへ送信される。
後は、パソコン側で、I信号、Q信号による位相が直交する実信号電圧デジタル値を復調計算して、その計算値をDA変換して、文字、画像等に表示したり、音声を出したりするだけ。
簡単にはこれだけの原理なのに、ネット上には非常に難しい説明が良く見られる。
以下はネットでよく見かけるヒルベルト変換の図と説明。
こうした説明は(おそらく)失敗事例ではないだろうか。
SDRに入力されるRF信号を直交する実信号電圧で表現する場合、その信号電圧成分は、実数部がI(t), 虚数部がQ(t)で、複素数座標上を時間的にリアルタイムで移動しているとも解釈できる。
従って、一番下の得たい目的信号 Real Part = I(t), Imaginary Part = Q(t) の信号は、図に書かれた極座標値(A(t), θ(t))を計算して求める計算はしないはずである。
ところが、上の「ヒルベルト変換」の説明は、あたかもSDR内で、この図にかかれている「ヒルベルト変換」演算を実行することで、I(t)、Q(t)信号を計算しているように説明されている。
こうしたネット上の解説は、適切とは考えにくいように思う。
とくに最初にSDRがどんな仕組みで動くのか知りたい僕らビギナー達がこの記事を読んだら、大変やっかいな迷宮へ入り込まされる甚大な被害を受けると思う。
この説明ではさっぱりわからないと思われる。
この説明ではさっぱりわからないと思われる。
厄介な考え方は、最初の1行目。
”この世に存在する信号は全て実信号であり、”・・・この文章からは、記事の筆者は、電波で届く変調信号が実数電圧信号だけで構成され、複素数表現による電波信号の存在を完全に否定していることがわかる。
これでは、現在までの複素数を基礎とする数学、物理学、電気・電子工学の学問体系全体の複素数の基礎が根本から理論的に崩れてしまうようにも解釈できると思う。
これは、日本国内で行われてきた教育に関わる法律で、「虚数は存在しないものとして教えなさい。」決めていることが、現在でも僕らに悪影響を及ぼしている結果のようにも思える。
上の筆者による計算式は、本当に「ヒルベルト変換」なのかどうかも、はっきりしない。
式だけを見ると、単に直交座標から極座標変換の計算式になっている。
すなわち、極座標の直径r(t)と、位相角θ(t)を、I(t),Q(t)から計算して求める式になっている。
ところが、この「ヒルベルト変換」の説明文に、I(t)値からQ(t)値を求めるという説明があるため、式と文章説明文の間に矛盾があり、読み手の僕らは、この矛盾にひっかかり、わからなくなる。
かつ複素数を存在しないものとする、おそらくは誤った教育による厄介な先入観を思いこんでしまった筆者の専門的説明を疑い無く鵜呑みに読んで理解に失敗した。・・・とも思える。
それであれば、筆者の考えや教育機関による教育指導内容の根幹を見直し、最初に、電気信号は複素数平面に存在すると考えるか、または複素数平面上にその存在を表現できると考えて、複素数表現で計算式にできることを仮定したほうが、これまでの日本国内の虚数または複素数を基礎とする全ての学問上の数学的矛盾を解決できるように思える。
恐らくオイラーさんが300年近くも前に証明している内容を、未だに僕らは、混乱した情報に振り回されているように思える。
僕は、ここにおいても、以前出くわしたように、日本の数学教育が、複素数定義の根本で壊れているところがある、とあらためて思った。
以下、現在見つかっているもっともそれらしき「ヒルベルト変換」の説明資料。
デザインウェーブ誌(CQ出版社出版 廃刊)から、引用。
(Copyright by Design Wave magazine, CQ Pub.inc.)
要するに、入力信号を複素信号成分 (Re,Im)=(I,Q) の2相電圧を取り出すのが「ヒルベルト変換」なのではないかと思われた。・・・が・・・。
上図Z変換第グラムの正誤は確認中で正しいかどうかわからないが、概念をつかむには現在のところ一番良い資料と思われる。(・・・と思ったが、幸運にも最良の資料が見つかった。[1])
なお、定数と思われるK1,K2,K3等のZ変換ブロックがこのままでは機能しないと思う。今後の課題として検討を進めるヒントとなった。
(図10図の遅延回路の出力 Iと、「ヒルベルト変換」フィルタの出力(I,Q)で、出力Iが重複し、おかしな図になっているので注意要。ここのI信号の遅延回路はヒルベルト変換回路のQ出力遅延時間と同じ遅延時間がかかるようになっていると考えます。)
「ヒルベルト変換」の定義式が見つかった。
まさに、トロント大学の Frank R. Kshischang さんが、ヒルベルト変換定義式を書いていた。[1]
ベースバンド信号を関数g(t)とすると、信号1/(πt)との畳み込み積分で定義されている。
ここでの畳み込み演算の信号処理上の意味は、ベースバンド信号g(t)の応答を、関数1/(πt)による一種のサンプリング信号(”時間tに反比例して減衰する重み関数(忘却関数)信号”)により計算していると解釈しています。
ここでの畳み込み演算の信号処理上の意味は、ベースバンド信号g(t)の応答を、関数1/(πt)による一種のサンプリング信号(”時間tに反比例して減衰する重み関数(忘却関数)信号”)により計算していると解釈しています。
この計算式に従ってMPU/DSPで数値演算すれば、ベースバンド信号x(t)は、それと直交関数x(t)^が求まるので、位相-90度シフト信号を得るために、国内で有名と聞くメリーゴーランド式、メリゴ式に見られる”PSN方式SSB変調器”のPoly Phase Filter の利得と周波数特性の補正で苦労する必要も無くなってしまうことが分かった。
(メリーゴーランド式というのは、基礎構造は従来PSN方式と同機能と考えます。従来のPSN方式との違いは、ミキサーを4層クロック制御のアナログスイッチで置き換えたものと考えます。ただしこのメリゴ式ミキサーではそれ相当のスイッチング・ノイズの発生が起こる課題が未解決であること、複素信号処理には90度位相のずれた2層クロックだけですむ複素数信号処理の概念発見にいたらず、後のNokia社による革新的特許のI,Q信号概念(1997年)はわかっていなかった点が惜しまれる点と読み取りました。)
(メリーゴーランド式というのは、基礎構造は従来PSN方式と同機能と考えます。従来のPSN方式との違いは、ミキサーを4層クロック制御のアナログスイッチで置き換えたものと考えます。ただしこのメリゴ式ミキサーではそれ相当のスイッチング・ノイズの発生が起こる課題が未解決であること、複素信号処理には90度位相のずれた2層クロックだけですむ複素数信号処理の概念発見にいたらず、後のNokia社による革新的特許のI,Q信号概念(1997年)はわかっていなかった点が惜しまれる点と読み取りました。)
この文献[1]には、ヒルベルト変換の関数の性質が表にまとまっていて、A*sin(ω*t)の直交関数も書かれている。任意のベースバンド信号は、任意の周波数成分の定数倍したフーリエ級数 Σ Ai*sin(ωi*t) {i=1,2,3,...n} で表現できるので、「ヒルベルト変換」数値演算により、そうした入力信号の束を一括して直交関数信号に変換できると解釈した。
応用例:
おじさん工房のSSB復調器の255 Tap IIRによる「ヒルベルト変換」演算がFPGAにプログラムされ、同演算にかかる遅延回路とともに、ベースバンド復調信号を取り出している例がある。[2]http://ojisankoubou.web.fc2.com/apb-1/radio.html
上の例では、「ヒルベルト変換」演算を行った出力信号は、行わないI信号の1/2の電圧が得られているため、I信号を2倍利得のAFアンプで増幅すれば期待される復調電圧が得られます。
これなら「ヒルベルト変換」演算による信号の遅延時間や位相づれずも気にしなくてすみます。
一方、SSB変調でPSN方式をとる場合、IQ変調器に与えるQ信号の計算に「ヒルベルト変換」演算をしたQ信号を与えれば、Poly Phase Filter 90度位相シフト回路の代わりにでき、PPFの帯域利得が一定でない課題を解決する効果が得られます。
Weaver式PSN変調方式では、「ヒルベルト変換」が不要になる原理上のメリットがあることも判明しました。(別記事に記載済)
参考記事:
複素数電圧平面上の交流電圧の時間関数の動き 交流の正体をつかむ
http://ji1nzl-official.blogspot.jp/2015/12/blog-post_9.html
参考文献:
[1] The Hilbert Transform, Mr. Frank R. Kshischang
参考文献:
[1] The Hilbert Transform, Mr. Frank R. Kshischang
Copyright by Mr. Frank R. Kshischang,The university of Toronto Oct.22, 2006
[2] APB-1を使ったラジオ受信機(Software Defined Radio)
http://ojisankoubou.web.fc2.com/apb-1/radio.html
Copyright by Ojisan Kobo inc.(おじさん工房さん)
謝辞:
Special thanks to
Mr. Frank R. Kshischang,The university of Toronto, Canada
Serching service by Google inc.,
Design Magazine CQ Pub. inc,
Mr. Nishimura, AOR inc.,
Ojisan Kobo inc.
Ojisan Kobo inc.
デザインウェーブ誌(既に廃刊)からヒルベルト変換の資料を引用して、同機能の概念を概説。
2016/7/31
トロント大学 Frank R. Kshischang さんのヒルベルト変換式定義について概説追加。
2016/8/30
ヒルベルト変換をキーにネット検索すると多数の学術文献が見つかる。しかし、内容の信頼性の確認できるものは、日本国内では現在でも決め手となる文献は全くないと思う。
前記、トロント大学 Frank R. Kshischang さんのヒルベルト変換式は、数学的定義式そのもを曖昧無く書いており、現在、一番優れた解説になっている。
2016/9/18
・おじさん工房のヒルベルト変換の応用例を追記。
・国内の文献で「ヒルベルト変換」が検索にかかるようになりました。
下の文献は、積分記号が入力漏れになったままのようです。(未修正?)
「ヒルベルト変換」のアルゴリズムが書かれているのがプログラミング上の参考になりそうです。(僕について再現性は現在未確認です。)
CSD 表現 FIR フィルタを用いたヒルベルト変換器の設計 フィルタを用いたヒルベルト変換器の設計 フィルタを用いたヒルベルト変換器の設計
Hilbert Transformer Design Using CSD FIR Filter
(Copyright) Yasuhiro Takahashiさん, Tatsuo Kitajimaさん, Kazukiyo Takahashiさん
http://www1.gifu-u.ac.jp/~yasut/pdf/iee_paper.pdf
2020/10/4
複素信号は、複素数平面で、複素共役の正と負の周波数の複素数電圧成分により、実数軸上の振動する電圧に見える実数電圧として構成されています。
これは一つの複素数平面でも、そこから位相が傾いた複素数平面で、同じく相対的に複素共役の正と負の周波数の複素数電圧’で構成されていることが数学の計算で容易に求まります。
国内の関連の物理学、通信技術理論は現在まで整理されておらず、ばらばらの理論解説で、誤りが多数見られますので、慎重な注意が必要です。
Return to INDEX
-----------------------------------------------------------------------------------------------------------------------------
かなり困っていること:
日本の各種専門誌、教科書、ウェブ上の専門教育記事、電子情報学会等の論文等、再現性が確認できない、正誤のかなり妖しいものや、または完全な論理ミスも相当数あり、大変困っています。
そうした場合は、結果としてそれを読まないほうが良く、無駄な時間と誤った情報に悩まされずにすむので、かなりの重症を負った文化状況があるように思うことが多いです。
ネット検索でも閲覧数が多いサイトが上位に上がってくる傾向があり、そうした上位ランクのサイトに致命的論理ミスが大変沢山混入している事象が見られます。
信じられないほど高度で価値のある情報が発見される場合と、鵜呑みにして信じると騙されて沢山時間と費用を無駄にしてしまう場合とがあります。
できれば誤情報が発信されないような文化の底上げ(教育の質の改善)が必要なのかもしれないと思います。
人は誰でも誤りをしてしまうのでそれは仕方ないとしても、誤りがあってもそれを知りながら何も言わないと、誰も何も修正せず、放置されたまま誤りが繰り返し語り継がれ、ずっと後の世代へ負の文化遺産として残ってしまっています。
それなので、誤りに気づいた時点で、誤り(書籍や論文、放送内容、言ったこと、書いたこと等)を修正することは大変大切な作業と思います。
日本国内に少なくとも江戸時代から久しくあると思われる考え方「見ざる、言わざる、聞かざる」、(都合の悪いことは、それがわかっても)「無かったことにする。」という仕事の仕方、そうした物の考え方、課題へ対する姿勢は良くない風習(文化)なので、問題や課題を改善する方向で、未来指向で考えることが大切で、文化・文明の発展に効果があると感じる今日この頃です。
Return to INDEX
-----------------------------------------------------------------------------------------------------------------------------
かなり困っていること:
日本の各種専門誌、教科書、ウェブ上の専門教育記事、電子情報学会等の論文等、再現性が確認できない、正誤のかなり妖しいものや、または完全な論理ミスも相当数あり、大変困っています。
そうした場合は、結果としてそれを読まないほうが良く、無駄な時間と誤った情報に悩まされずにすむので、かなりの重症を負った文化状況があるように思うことが多いです。
ネット検索でも閲覧数が多いサイトが上位に上がってくる傾向があり、そうした上位ランクのサイトに致命的論理ミスが大変沢山混入している事象が見られます。
信じられないほど高度で価値のある情報が発見される場合と、鵜呑みにして信じると騙されて沢山時間と費用を無駄にしてしまう場合とがあります。
できれば誤情報が発信されないような文化の底上げ(教育の質の改善)が必要なのかもしれないと思います。
人は誰でも誤りをしてしまうのでそれは仕方ないとしても、誤りがあってもそれを知りながら何も言わないと、誰も何も修正せず、放置されたまま誤りが繰り返し語り継がれ、ずっと後の世代へ負の文化遺産として残ってしまっています。
それなので、誤りに気づいた時点で、誤り(書籍や論文、放送内容、言ったこと、書いたこと等)を修正することは大変大切な作業と思います。
日本国内に少なくとも江戸時代から久しくあると思われる考え方「見ざる、言わざる、聞かざる」、(都合の悪いことは、それがわかっても)「無かったことにする。」という仕事の仕方、そうした物の考え方、課題へ対する姿勢は良くない風習(文化)なので、問題や課題を改善する方向で、未来指向で考えることが大切で、文化・文明の発展に効果があると感じる今日この頃です。



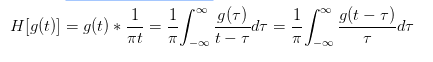
0 件のコメント:
コメントを投稿
現在コメント機能に不具合が出ています。お手数ですみません。
メッセージは、メールでお送り願います。