実測すると、約21mの長さの半波長ダイポールは、長さを調整することで、7MHz帯においてVSWR=1.0に近い値になりました。
一方、同じアンテナは、21MHz帯では、VSWR実測値は 2.0〜3.0を簡単に上回り、使えないことは無いのですが、反射電力が多く送信時には問題がありました。
この現象では何が起こっているのか? 私は、仮説として、『アンテナは、使用する電波の周波数により、インダクタンス値、キャパシタンス値が変化する。』と考え、モーメント法を使った著名なアンテナシミュレータMMANAと、電子回路シミュレータLTspiceで、この仮説が正しいかどうか、検証してみました。
その結果、この仮説はどうやら正しそうで、実測とも合うという結果を得ました。
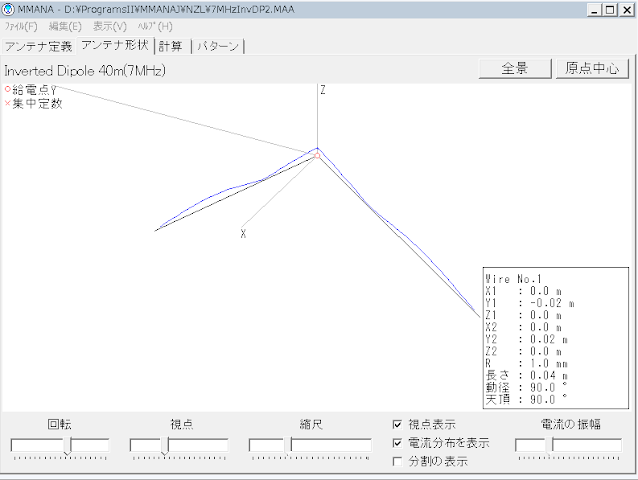
これは、7MHz 逆V型ダイポールアンテナの全景と、その電流分布をMMANAで使用周波数=7.05MHzの条件でシミュレートして描かせたものです。このように、水平ダイポールのインピーダンス73Ω(理論値)は、逆V型に角度を持たせ、その角度を調整すると、インピーダンスを50Ωに整合でき、特性インピーダンス50Ωの5D2Vなどの同軸ケーブルを接続すると、VSWR≒1.0でほぼ理想的条件で大電力の送信アンテナにも使用できるようになります。これは実測と一致しました。
これは上と同じ7MHz 逆V型ダイポールアンテナの全景と、その電圧分布をMMANAで使用周波数=21.20MHzの条件でシミュレートして描かせたものです。青線の電流分布を見ると、アンテナ中央部で最大、アンテナ末端で最小となり、かなり良く同調している様子が見られます。
このグラフは、MMANAで計算した7MHz半波長ダイポールの7.05MHzでのインピーダンス抵抗成分R、リアクタンス成分jXです。同アンテナは、7.05MHzにて同調し、R=46.99823[Ω], jX=0[Ω], L=18.7[μH],C=27.2[pF]と計算結果が出ました。
このグラフは、MMANAで計算されたR,L,C直列回路を、5MHz〜9MHzの範囲で、利得値と位相値を描かせたものです。
MMANAで計算されたR,L,C値によるR,L,C直列回路は、7.05MHzにて最大利得0dBとなり、位相が大きく変化する位相グラフの変曲点を通過し、うまく同調していることがわかります。
このグラフは、MMANAで計算した7MHz半波長ダイポールの21.20MHzでのインピーダンス抵抗成分R、リアクタンス成分jXです。同アンテナは、同調周波数は約22MHzまで離調し、R=128.358[Ω], jX=0[Ω], L=14.4[μH],C=3.6[pF]と計算結果が出ました。
同調周波数が、約22MHzまで離調し、高周波抵抗成分R=128.358[Ω]では、同軸ケーブルの特性インピーダンス50[Ω]から大きくずれてしまいます。このため、インピーダンス整合回路を使わないとVSWR≒6と高く、大電力送信はできません。
このグラフは、MMANAで計算されたR,L,C直列回路を、15MHz〜30MHzの範囲で、利得値と位相値を描かせたものです。
MMANAで計算されたR,L,C値によるR,L,C直列回路は、21.987MHzにて最大利得 約-2dBとなり、位相が大きく変化する位相グラフの変曲点を通過し、21.200MHzからかなり離調していることがわかります。
実効利得は、MMANAにて約5dBと計算され利得は申し分ない値です。
しかし、同調周波数ずれと、抵抗成分が100Ω以上となるので、送信用にはインピーダンスマッチング回路は必須となる、という結果を得ました。
以上のように、従来言われてきた7MHz用半波ダイポールは、インピーダンスマッチング回路を使用するという条件付きで利用は可能であること。
『アンテナは、使用する電波の周波数により、インダクタンス値、キャパシタンス値が変化する。』という私の仮説は、それに加えて(高周波)抵抗値も変化するという結果を得ました。
(このアンテナの性質は、分布定数回路として公知のものですが、学校教育レベルでは扱われていない場合が多いようです。同じ問題は、非常に高い周波数SHF以上で、部品サイズが波長の長さに近づくときに起こるようです。詳細は分布定数回路を調査ください。)
Revision
0.1 : 06/19/2017
アンテナの共振周波数式の誤りを削除
誤り:f=1/(2*π)*√(1/LC)-(R/2L)^2) ...この式は、過渡現象でRLC回路から輻射される電波の周波数
正:アンテナの共振周波数: f=1/(2*π)*√(1/LC)





0 件のコメント:
コメントを投稿
現在コメント機能に不具合が出ています。お手数ですみません。
メッセージは、メールでお送り願います。