1.微分回路の動作確認
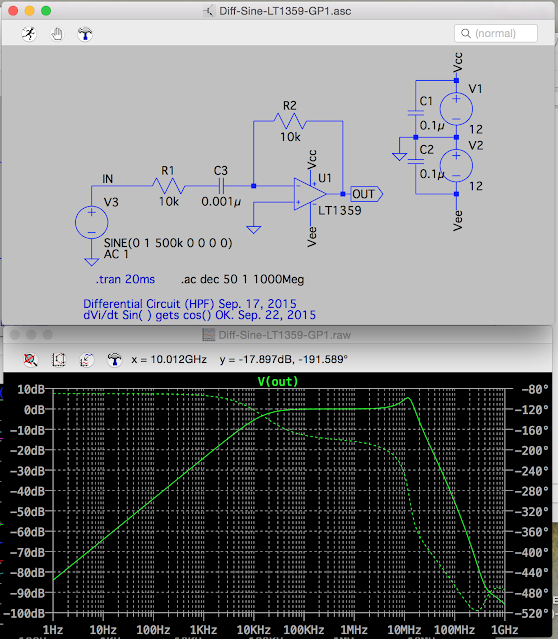
(1)微分回路(HPF)の利得・位相特性
Fc=1/(2*π*R*C)=1/(2*π*10*10^3*0.001*10^(-6))=15.9[KHz]
以上の周波数の交流信号を通過させる。
一方、オペアンプ利得特性から上限の利用可能周波数は、約3[MHz]が上限。
通過帯域= 16[KHz]〜3[MHz]
遮断周波数 Fc [Hz]以下のフィルターされる周波数領域に、ωに比例して利得が直線的に増幅し、かつ位相ずれが90度になっている領域がある。
周波数軸は対数軸になっているが、この直線的利得増加と位相ずれ90度の特性が微分回路と呼ばれるゆえんとなる特性と考えられる。
しかしながら、通過帯域周波数は遮断周波数より上の周波数領域を使用する。このため、この微分回路を利用する実用周波数領域では、微分動作は発生しないことになる。(※1)
(2)500[KHz]サイン波高周波電圧入力時の過渡解析結果
出力信号電圧は、サインを微分した位相90度ずれたコサイン信号にω=2*π*500x10^3を乗算した電圧値を期待したいが、そう成るには、ωを乗算しなければならない。しかし、周波数に比例して出力電圧を上げることはこの回路では不可能なので、数学的な微分演算は原理的に出来ない。
不明点:何故、この回路を微分回路と呼ぶのだろうか?
(※1) -> 遮断周波数以下の利用されない周波数領域で微分動作が起こることが判明した。
(Oct.4, 2015)
(※1) -> 遮断周波数以下の利用されない周波数領域で微分動作が起こることが判明した。
(Oct.4, 2015)
(3)矩形波信号入力時の過渡解析結果
数学的には、矩形波立ち上がりで、電圧最大値+12Vを期待したいが、出力電圧瞬時値=2.0[V]の時間幅の狭いパルス信号しか得られない。数学的微分動作は無理そうである。
矩形波の立ち下がりも同様、電圧値最小値-12Cを期待したいが、出力電圧瞬時値=-2.0[V]の狭い矩形波の狭いパルス信号しか得られない。同様に、数学的微分動作は無理という結果となった。
不明点:結局、微分回路と呼ばれるものは、HPF(High Pass Filter)と解釈して利用するしかないのだろうか?
2.積分回路の動作
Fc=1/(2*π*R*C)=1/(2*π*10*10^3*0.005*10^(-6))=3.18[KHz]
以下の周波数の交流信号を通過させる。
(1)1[KHz]サイン波電圧入力時の過渡解析結果
数学的積分では、定積分を連想させるが、どの区間の時刻の面積を求めているのかわからない。
不明点:何故、この回路を積分回路と呼ぶのだろうか?
出力信号は、位相が90度ずれているのは雰囲気として積分関数演算を連想させるが、数学的には、ωで除算した出力値にならねばならない。しかし、ωは周波数に比例して変化するのでそうした倍率を周波数に合わせて変化させるのは、この回路では数学的積分は出来ない。
また電圧の初期値も数学の演算値とは全く合わない。
(2)500[Hz]矩形波電圧入力時の過渡解析結果
数学的積分では、矩形波の面積を定積分することになるが、定積分すべき時間区間がわからない。波形は三角波に近づけば正しい結果のようにも思えるが、ωで除算するのが数学的積分なのに、電圧利得が固定になるので、数学的定積分は回路原理的に無理である。
出力電圧の初期値も数学的計算値とは全く合わない。
不明点:結局、積分回路と呼ばれるものは、LPF(Low Pass Filter)と解釈して利用するしかないのだろうか?
低い周波数領域のLPF帯域内では180度位相が一定して反転する。
Fcをかなり上回ると、90度位相が一定にずれるという興味深い位相特性が見られる。
ただし利得は対数表現の周波数に対して、直線的に減少している。この領域では、積分動作が起こっている。(※2)
電気回路で言われてきている微分回路、積分回路としては、これで期待動作なのかもしれないが、数学的微分、数学的積分とは計算が全く合わない。なぜこんなことになっているのだろう。この点、アナログコンピュータの微分・積分回路の動作はどうなのだろう?
※1,※2 ->
意外なことに、遮断周波数を堺にした通過周波数帯域外に、微分動作、積分動作する領域があることが判明した。
なんと、HPF, LPF として利用する周波数通過帯域の外側に、微分、積分の演算動作領域がある。
すなわち、微分回路、積分回路と呼ばれる演算を期待する場合は、遮断周波数を境にした通過帯域外の周波数でこれらの回路を、微分演算、積分演算に利用できることが明らかになってきた。





0 件のコメント:
コメントを投稿
現在コメント機能に不具合が出ています。お手数ですみません。
メッセージは、メールでお送り願います。